The Quantum Insider (TQI) is the leading online resource dedicated exclusively to Quantum Computing.



The smaller electronic components become, the more complex their manufacture becomes. This has been a major problem for the chip industry for years. At TU Wien, researchers have now succeeded for the first time in manufacturing a silicon-germanium (SiGe) transistor using an alternative approach that will not only enable smaller dimensions in the future, but will also be faster, require less energy and function at extremely low temperatures, which is important for quantum chips.
The key trick lies in the oxide layer that insulates the semiconductor: it is doped and produces a long-range effect that extends into the semiconductor. The technology was developed by TU Wien (Vienna), JKU Linz and Bergakademie Freiberg. The results have now been published in the journal IEEE Electron Device Letters and selected as Editor’s Pick on the cover of the August issue.

Quantum technologies are systems that can compute data, sense their surrounding environment or perform other functions leveraging quantum mechanical effects. Connecting these technologies over long distances has so far proved challenging, as quantum information can easily become scrambled or destroyed following decoherence resulting from the systems’ interactions with their surrounding environment.
Over the past few years, quantum physicists and engineers have been trying to devise effective techniques to reliably establish quantum networks, infrastructures that allow quantum information to travel between different devices.
The realization of these networks requires so-called quantum relays, intermediate stations that can forward and redistribute entangled states, extending the distances across which devices can communicate.
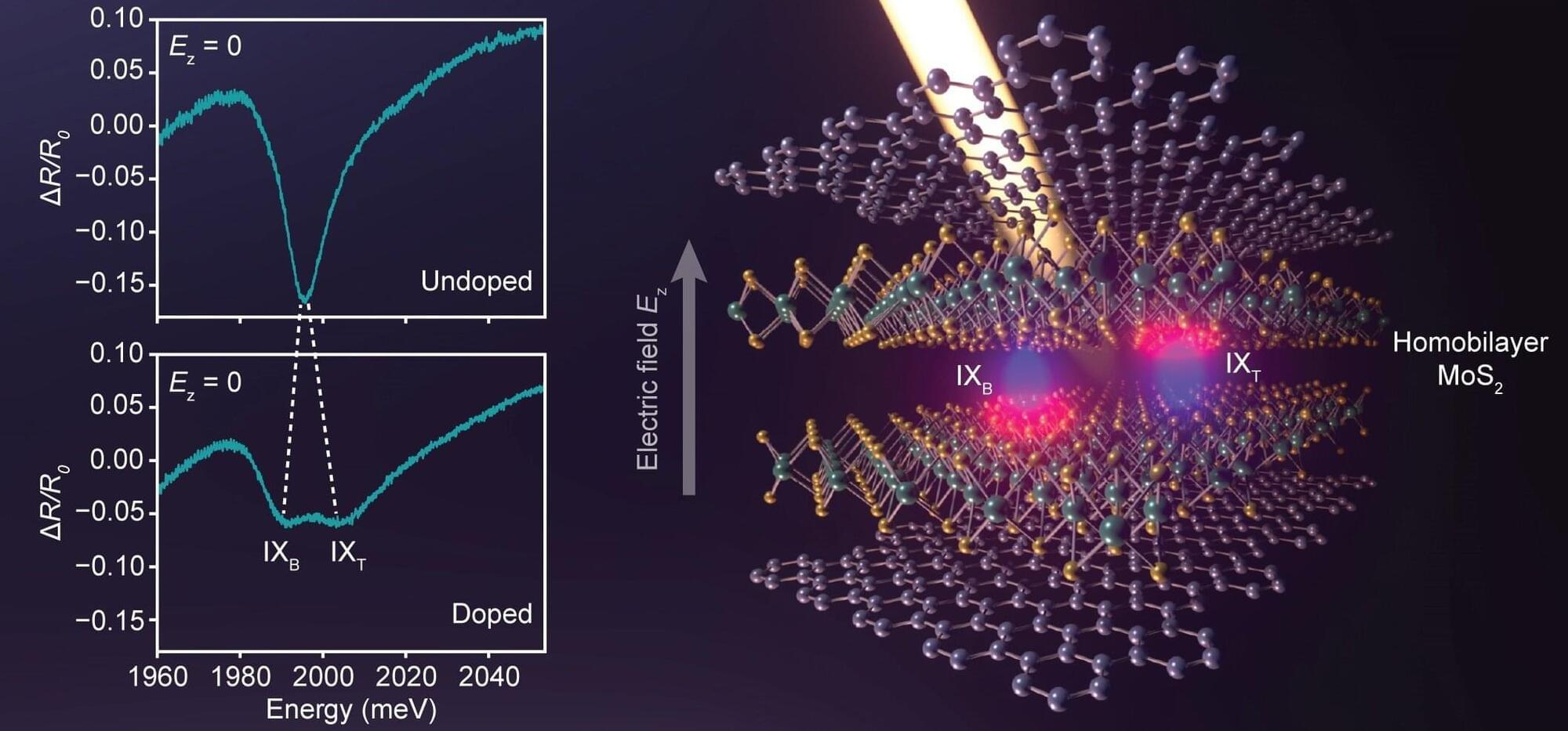
Excitons, bound states between an electron (i.e., a negatively charged particle) and a hole (i.e., the absence of an electron) in materials, are a key focus of condensed matter physics studies. These bound states can give rise to interesting and uncommon quantum physical effects, which could be leveraged to develop optoelectronic and quantum technologies.
Over the past few years, physicists have observed a particular type of excitons, known as interlayer excitons, in various materials with two layers (i.e., bilayer materials). An interlayer exciton is a bound state between an electron and a hole that reside in two different layers of a material.
Researchers at Harvard University and other institutes recently observed an unconventional hybridization between interlayer excitons in a bilayer semiconductor, comprised of two layers of molybdenum disulfide (MoS₂).

The neutral atom array architecture for quantum computing has been rapidly advancing over the last several years, and a recent study published in Nature has just revealed another step forward for this technology. The team of Harvard researchers involved in this study have engineered a 3,000-qubit neutral atom array system capable of operating continuously for more than two hours, which goes far beyond typical trap lifetimes of only about 60 seconds.
Typically, neutral atom array systems arrange neutral atoms, like rubidium, in an array using highly focused laser beams, called optical tweezers. The individual atoms are arranged and held under vacuum conditions and then used as qubits to perform quantum computing and other operations. However, the procedure results in the loss of some atoms.
“An outstanding challenge associated with these systems involves atom loss, originating from errors in entangling operations, state-readout, and finite trap lifetime. Atom losses necessitate pulsed operation which limits the performance of these quantum systems, including the circuit depth of quantum computation, accuracy of atomic clocks, and the rate of entanglement generation in quantum networking protocols,” the study authors explain.

Nature has many rhythms: the seasons result from Earth’s movement around the sun, the ticking of a pendulum clock results from the oscillation of its pendulum. These phenomena can be understood with very simple equations. However, regular rhythms can also arise in a completely different way—by themselves, without an external clock, through the complex interaction of many particles. Instead of uniform disorder, a fixed rhythm emerges—this is referred to as a “time crystal.”
Calculations by TU Wien (Vienna) now show that such time crystals can also be generated in a completely different way than previously thought. The quantum physical correlations between the particles, which were previously thought to be harmful for the emergence of such phenomena, can actually stabilize time crystals. This is a surprising new insight into the quantum physics of many-particle systems.
The findings are published in the journal Physical Review Letters.

The artificial intelligence models that turn text into images are also useful for generating new materials. Over the last few years, generative materials models from companies like Google, Microsoft, and Meta have drawn on their training data to help researchers design tens of millions of new materials.
But when it comes to designing materials with exotic quantum properties like superconductivity or unique magnetic states, those models struggle. That’s too bad, because humans could use the help. For example, after a decade of research into a class of materials that could revolutionize quantum computing, called quantum spin liquids, only a dozen material candidates have been identified. The bottleneck means there are fewer materials to serve as the basis for technological breakthroughs.
Now, MIT researchers have developed a technique that lets popular generative materials models create promising quantum materials by following specific design rules. The rules, or constraints, steer models to create materials with unique structures that give rise to quantum properties.

Integration into a quantum money protocol shows that memories can now handle very demanding applications for quantum networking.
Researchers at the Kastler Brossel Laboratory (Sorbonne Université, CNRS, ENS-Université PSL, Collège de France), together with colleagues from LIP6 (Sorbonne Université, CNRS), have taken a major step forward in quantum technology: for the first time, they have integrated an optical quantum memory into a cryptographic protocol. This achievement, based on Wiesner’s unforgeable quantum money scheme, demonstrates that quantum memories are now mature enough to operate under very demanding conditions for networking.
In a study published on September 19 in Science Advances, the Paris team implemented Wiesner’s quantum money, a foundational idea in quantum cryptography that relies on the no-cloning theorem to prevent counterfeiting. Unlike previous demonstrations that bypassed storage, this experiment incorporated an intermediate memory step—an essential capability for real-world applications where quantum data must be held and released on demand.

Dark Matter remains one of the biggest mysteries in fundamental physics. Many theoretical proposals (axions, WIMPs) and 40 years of extensive experimental search have not explained what Dark Matter is. Several years ago, a theory that seeks to unify particle physics and gravity introduced a radically different possibility: superheavy, electrically charged gravitinos as Dark Matter candidates.
A recent paper in Physical Review Research by scientists from the University of Warsaw and the Max Planck Institute for Gravitational Physics shows that new underground detectors, in particular the JUNO detector that will soon begin taking data, are well-suited to detect charged Dark Matter gravitinos even though they were designed for neutrino physics. Simulations that bridge elementary particle physics with advanced quantum chemistry indicate that a gravitino would leave a signal in the detector that is unique and unambiguous.
In 1981, Nobel Prize laureate Murray Gell-Mann, who introduced quarks as fundamental constituents of matter, observed that the particles of the Standard Model—quarks and leptons—appear within a purely mathematical theory formulated two years earlier: N=8 supergravity, noted for its maximal symmetry. N=8 supergravity includes, in addition to the Standard Model matter particles of spin 1/2, a gravitational sector with the graviton (of spin 2) and 8 gravitinos of spin 3/2. If the Standard Model is indeed connected to N=8 supergravity, this relationship could point toward a solution to one of the hardest problems in theoretical physics — unifying gravity with particle physics. In its spin ½ sector, N=8 supergravity contains exactly 6 quarks (u, d, c, s, t, b) and 6 leptons (electron, muon, taon and neutrinos), and it forbids any additional matter particles.

In an article published in Communications Physics, researchers from the Université libre de Bruxelles and the Institute for Quantum Optics and Quantum Information in Vienna present a new framework for describing physics relative to quantum reference frames, unveiling the importance of previously unrecognized “extra particles.”
In any experiment, specifying a physical quantity of interest always relies on a reference frame. For example, identifying the time at which an event happens only makes sense relative to a clock. Similarly, the position of a particle is usually defined relative to other particles. Reference frames are typically treated as classical systems, that is, they are assumed to have definite values when measured relative to other reference frames.
However, as far as we know, every system is ultimately quantum. As such, it can, in principle, exist in indefinite states called quantum superpositions. What does the physical world look like when described from the perspective of a reference frame that can be in a quantum superposition? Can we define consistent rules for changing between different perspectives?