Whether it is a cube of sugar or a chunk of a mineral, a mathematical analysis can identify how many fragments of each size any brittle object will break into


Go to https://ground.news/sabine to get 40% off the Vantage plan and see through sensationalized reporting. Stay fully informed on events around the world with Ground News.
In quantum physics, a wave function is a mathematical way to describe everything in the universe. But since quantum physics emerged, physicists have argued about whether or not the wave function is real. A group of physicists recently conducted a test of a theorem that describes the mechanics of the wave function, and they’ve told the press that they’ve settled the question: Yes, the wave-function is real. Let’s take a look.
Paper: https://arxiv.org/abs/2510.
👕T-shirts, mugs, posters and more: ➜ https://sabines-store.dashery.com/
💌 Support me on Donorbox ➜ https://donorbox.org/swtg.
👉 Transcript with links to references on Patreon ➜ / sabine.
📝 Transcripts and written news on Substack ➜ https://sciencewtg.substack.com/
📩 Free weekly science newsletter ➜ https://sabinehossenfelder.com/newsle… Audio only podcast ➜ https://open.spotify.com/show/0MkNfXl… 🔗 Join this channel to get access to perks ➜ / @sabinehossenfelder 📚 Buy my book ➜ https://amzn.to/3HSAWJW #science #sciencenews #quantum #physics.
👂 Audio only podcast ➜ https://open.spotify.com/show/0MkNfXl…
🔗 Join this channel to get access to perks ➜
/ @sabinehossenfelder.
📚 Buy my book ➜ https://amzn.to/3HSAWJW
#science #sciencenews #quantum #physics

Viazovska was born in Kyiv, the oldest of three sisters. Her father was a chemist who worked at the Antonov aircraft factory and her mother was an engineer. [ 6 ] She attended a specialized secondary school for high-achieving students in science and technology, Kyiv Natural Science Lyceum No. 145. An influential teacher there, Andrii Knyazyuk, had previously worked as a professional research mathematician before becoming a secondary school teacher. [ 7 ] Viazovska competed in domestic mathematics Olympiads when she was at high school, placing 13th in a national competition where 12 students were selected to a training camp before a six-member team for the International Mathematical Olympiad was chosen. [ 6 ] As a student at Taras Shevchenko National University of Kyiv, she competed at the International Mathematics Competition for University Students in 2002, 2003, 2004, and 2005, and was one of the first-place winners in 2002 and 2005. [ 8 ] She co-authored her first research paper in 2005. [ 6 ]
Viazovska earned a master’s from the University of Kaiserslautern in 2007, PhD from the Institute of Mathematics of the National Academy of Sciences of Ukraine in 2010, [ 2 ] and a doctorate (Dr. rer. nat.) from the University of Bonn in 2013. Her doctoral dissertation, Modular Functions and Special Cycles, concerns analytic number theory and was supervised by Don Zagier and Werner Müller. [ 9 ]
She was a postdoctoral researcher at the Berlin Mathematical School and the Humboldt University of Berlin [ 10 ] and a Minerva Distinguished Visitor [ 11 ] at Princeton University. Since January 2018 she has held the Chair of Number Theory as a full professor at the École Polytechnique Fédérale de Lausanne (EPFL) in Switzerland after a short stint as tenure-track assistant professor. [ 4 ] .


Most of us first hear about the irrational number π (pi)—rounded off as 3.14, with an infinite number of decimal digits—in school, where we learn about its use in the context of a circle. More recently, scientists have developed supercomputers that can estimate up to trillions of its digits.
Now, physicists at the Center for High Energy Physics (CHEP), Indian Institute of Science (IISc) have found that pure mathematical formulas used to calculate the value of pi 100 years ago has connections to fundamental physics of today—showing up in theoretical models of percolation, turbulence, and certain aspects of black holes.
The research is published in the journal Physical Review Letters.

Imagine having a continuum soft robotic arm bend around a bunch of grapes or broccoli, adjusting its grip in real time as it lifts the object. Unlike traditional rigid robots that generally aim to avoid contact with the environment as much as possible and stay far away from humans for safety reasons, this arm senses subtle forces, stretching and flexing in ways that mimic more of the compliance of a human hand. Its every motion is calculated to avoid excessive force while achieving the task efficiently.
In the MIT Computer Science and Artificial Intelligence Laboratory (CSAIL) and Laboratory for Information and Decisions Systems (LIDS) labs, these seemingly simple movements are the culmination of complex mathematics, careful engineering, and a vision for robots that can safely interact with humans and delicate objects.
Soft robots, with their deformable bodies, promise a future where machines move more seamlessly alongside people, assist in caregiving, or handle delicate items in industrial settings. Yet that very flexibility makes them difficult to control. Small bends or twists can produce unpredictable forces, raising the risk of damage or injury. This motivates the need for safe control strategies for soft robots.


When it comes to training robots to perform agile, single-task motor skills, such as handstands or backflips, artificial intelligence methods can be very useful. But if you want to train your robot to perform multiple tasks—say, performing a backward flip into a handstand—things get a little more complicated.
“We often want to train our robots to learn new skills by compounding existing skills with one another,” said Ian Abraham, assistant professor of mechanical engineering. “Unfortunately, AI models trained to allow robots to perform complex skills across many tasks tend to have worse performance than training on an individual task.”
To solve for that, Abraham’s lab is using techniques from optimal control—that is, taking a mathematical approach to help robots perform movements in the most efficient and optimal way possible. In particular, they’re employing hybrid control theory, which involves deciding when an autonomous system should switch between control modes to solve a task. The research is published on the arXiv preprint server.
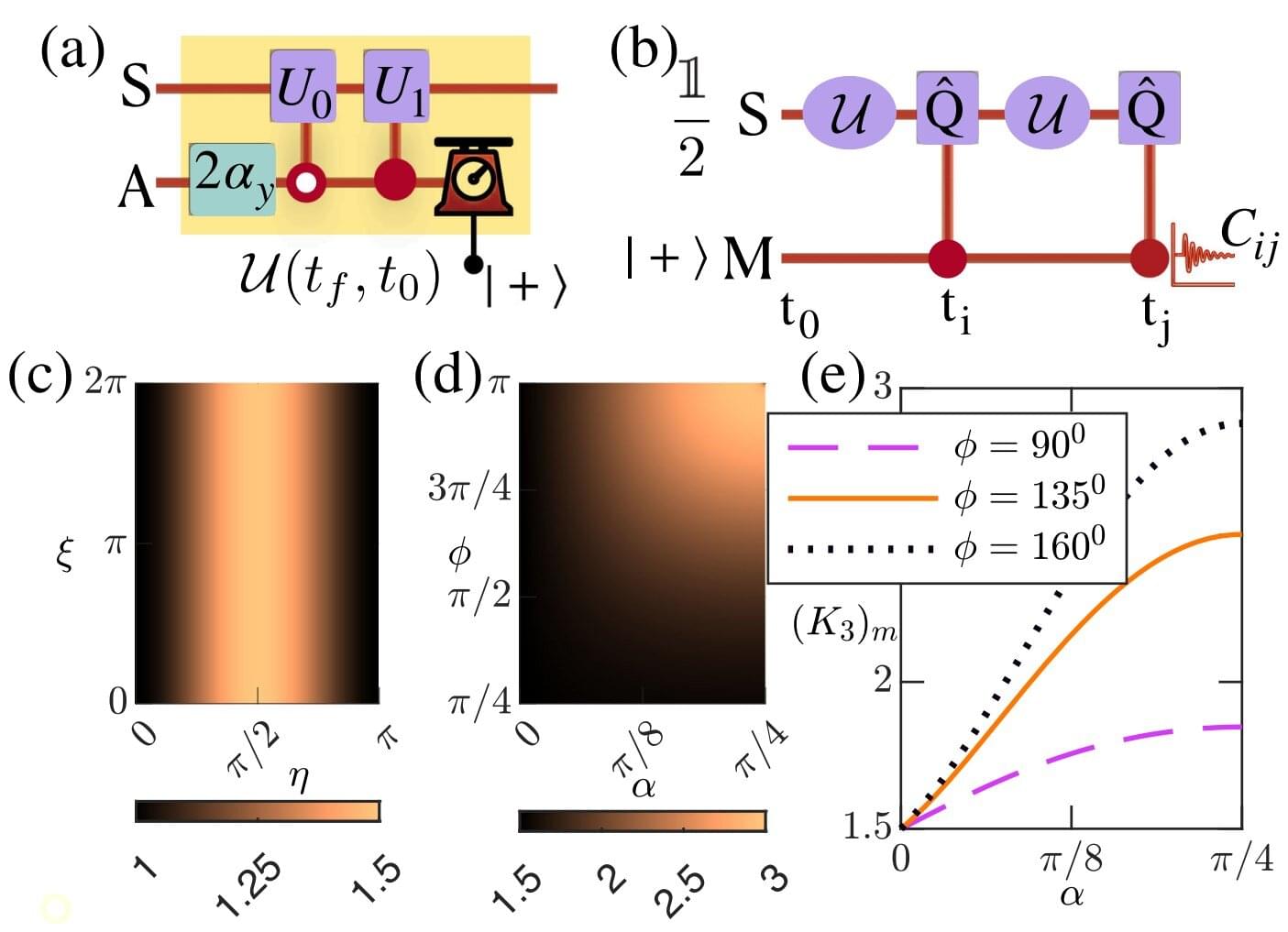
The quantum world is famously weird—a single particle can be in two places at once, its properties are undefined until they are measured, and the very act of measuring a quantum system changes everything. But according to new research published in Physical Review Letters, the quantum world is even stranger than previously thought.
What happens at the quantum level is in stark contrast to the classical world (what we see every day), where objects have definite properties whether or not we look at them, and observing them doesn’t change their nature. To see whether any system is behaving classically, scientists use a mathematical test called the Leggett-Garg inequality (LGI). Classical systems always obey the LGI limit while quantum systems violate it, proving they are non-classical.