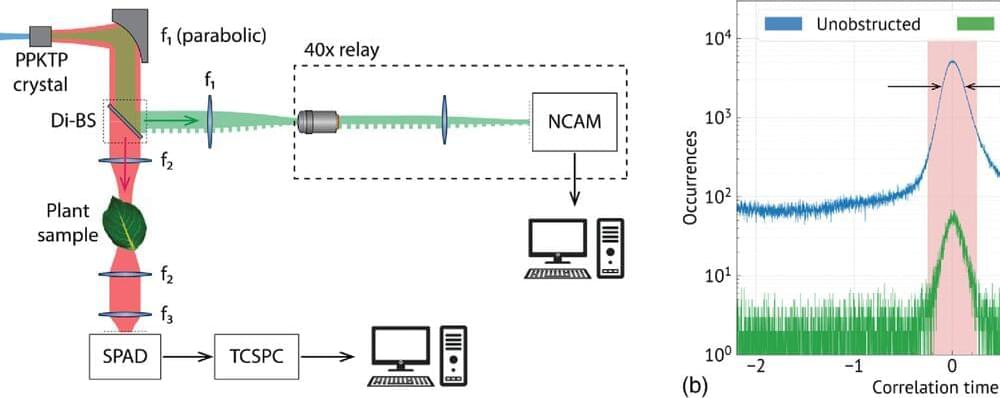
A study published in the journal Optica demonstrates live plant imaging of several representative plant samples, including the biofuel crop sorghum. By employing a novel detector, researchers obtained clear images of living sorghum plants with a light far dimmer than starlight. This advance enables imaging of delicate, light-sensitive samples, such as biofuel crops, without disturbing or damaging the plants.
A method called quantum ghost imaging (QGI) allows scientists to capture images at extremely low light levels. QGI also enables the use of one low intensity color, best matched to the sample and a different color at higher intensity, sufficient to form the image of the sample. This approach improves imaging in regions of light where traditional cameras struggle.
By using label-free infrared imaging, researchers can gather critical information about important plant processes, such as water content and photosynthesis, even in low-light conditions. This is particularly beneficial for studying biofuel crops, where researchers want to optimize plant growth and health to maximize yield and sustainability.