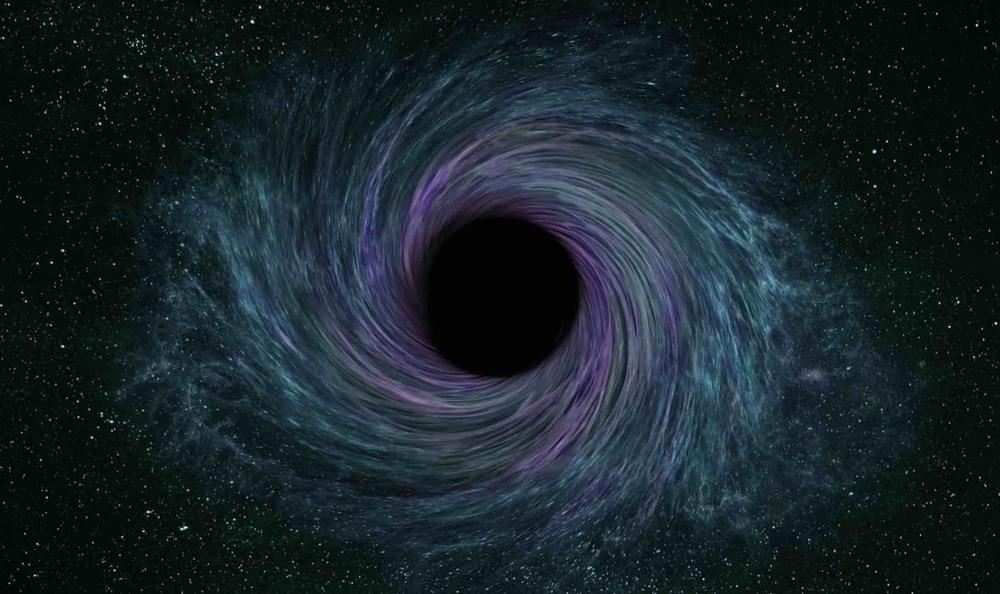
An artificial black hole produced using sound waves and a dielectric medium has been created in the lab, according to researchers with an international think tank featuring more than 30 Ph.D. research scientists from around the world.
The researchers say their discovery is significantly more cost-effective and efficient than current methods in use by researchers who want to simulate the effects of a black hole in a laboratory environment.
New York-based Applied Physics first achieved recognition with the 2021 publication of a peer-reviewed theoretical paper detailing the mathematics behind the construction of a physical warp drive. More recently, the organization published a method for using Cal Tech’s Laser Interferometer Gravitational-Wave Observatory (LIGO) to detect the use of warp drives in outer space, co-authored by Dr. Manfred Paulini, the Associate Dean of Physics at Carnegie Mellon University.