An experimental LLM from OpenAI solved some of the world’s hardest math problems at the 2025 International Math Olympiad, the company said.



IN A NUTSHELL 🐕 CARA is a robot dog created by a Purdue University student using innovative capstan drive technology. 🔧 The robot incorporates custom 3D-printed parts and high-strength materials like carbon fiber for durability and efficiency. 🤖 Advanced coding techniques such as Inverse Kinematics allow CARA to move with natural grace and agility. 🚀

Researchers have developed a technique that significantly improves the performance of large language models without increasing the computational power necessary to fine-tune the models. The researchers demonstrated that their technique improves the performance of these models over previous techniques in tasks including commonsense reasoning, arithmetic reasoning, instruction following, code generation, and visual recognition.
Large language models are artificial intelligence systems that are pretrained on huge data sets. After pretraining, these models predict which words should follow each other in order to respond to user queries. However, the nonspecific nature of pretraining means that there is ample room for improvement with these models when the user queries are focused on specific topics, such as when a user requests the model to answer a math question or to write computer code.
“In order to improve a model’s ability to perform more specific tasks, you need to fine-tune the model,” says Tianfu Wu, co-corresponding author of a paper on the work and an associate professor of computer engineering at North Carolina State University.



Modern-day computers have proved to be quite powerful in what they can do. The rise of AI has made things we previously only imagined possible. And the rate at which computers are increasing their computational power certainly makes it seem like we will be able to do almost anything with them. But as we’ve seen before, there are fundamental limits to what computers can do regardless of the processors or algorithms they use. This naturally leads us to ask what computers are capable of doing at their best and what their limits are. Which requires formalizing various definitions in computing.
This is exactly what happened in the early 20th century. Logicians & mathematicians were trying to formalize the foundations of mathematics through logic. One famous challenge based on this was the Entscheidungsproblem posed by David Hilbert and Wilhelm Ackermann. The problem asked if there exists an algorithm that can verify whether any mathematical statement is true or false based on provided axioms. Such an algorithm could be used to verify if any mathematical system is internally consistent. Kurt Gödel proved in 1931 that this problem could not be answered one way or the other through his incompleteness theorems.
Years later, Alan Turing and Alonzo Church proved the same through separate, independent means. Turing did so by developing Turing machines (called automatic machines at the time) and the Halting problem. Church did so by developing lambda calculus. Later on, it was proved that Turing machines and lambda calculus are mathematically equivalent. This led many mathematicians to theorize that computability could be defined by either of these systems. That in turn caused Turing and Church to make their thesis: every effectively calculable function is a computable function. In simpler terms, it states that any computation from any model can be carried out by a Turing machine or lambda calculus. To better understand the implications of the Church-Turing thesis, we need to explore the different kinds of computational machines.


Since its development 100 years ago, quantum mechanics has revolutionized our understanding of nature, revealing a bizarre world in which an object can act like both waves and particles, and behave differently depending on whether it is being watched.
In recent decades, researchers exploring this wave-particle duality have learned to measure the relative “wave-ness” and “particle-ness” of quantum objects, helping to explain how and when they veer between wave-like or particle-like behaviors.
Now, in a paper for Physical Review Research, researchers at the Stevens Institute of Technology report an important new breakthrough: a simple but powerful formula that describes the precise closed mathematical relationship between a quantum object’s “wave-ness” and “particle-ness.”
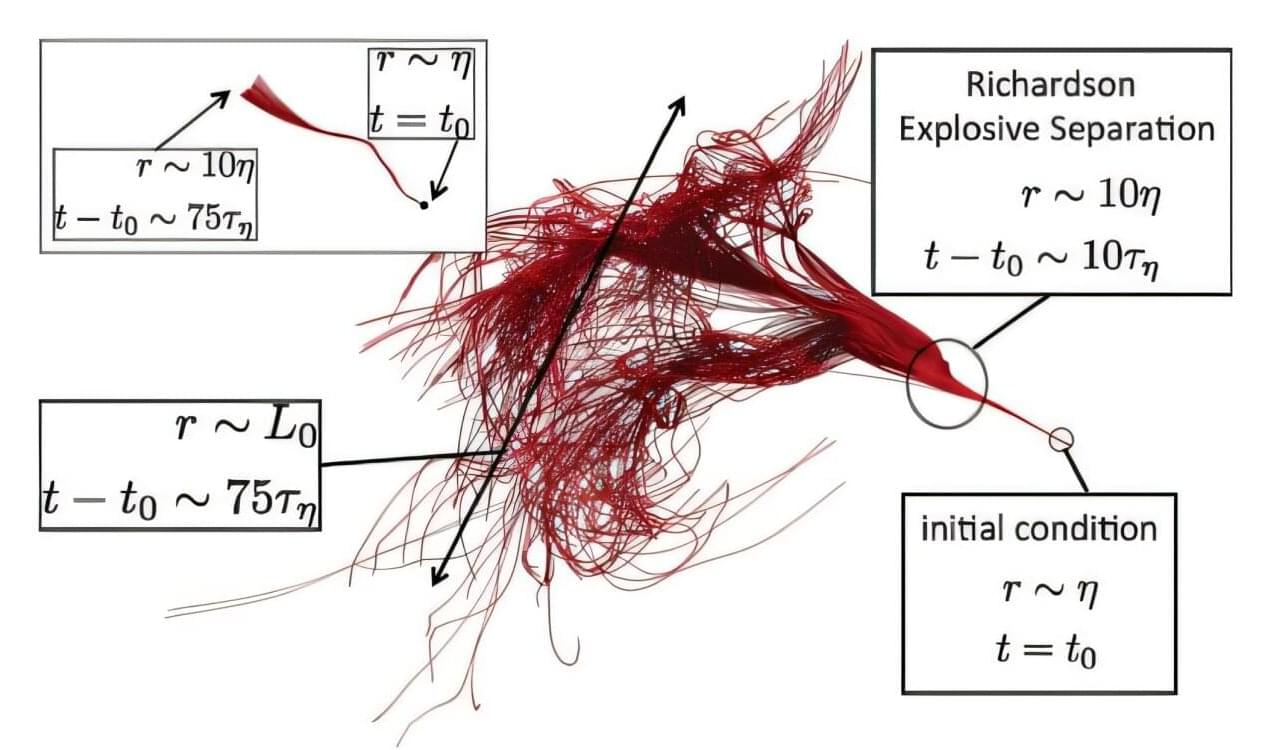
A sneeze. Ocean currents. Smoke. What do these have in common? They’re instances of turbulence: unpredictable, chaotic, uneven fluid flows of fluctuating velocity and pressure. Though ubiquitous in nature, these flows remain somewhat of a mystery, theoretically and computationally.
“Most flows that we encounter in nature are turbulent—it does not matter whether it is the flow outside the airplane that makes us fasten our seatbelts, or the flow in a small stream,” said UC Santa Barbara mathematics professor Björn Birnir.
“Turbulence is difficult to understand because the mathematical models that describe it are nonlinear, stochastic and the solutions are unstable. This made it necessary to develop new theories to truly understand the nature of turbulence.”