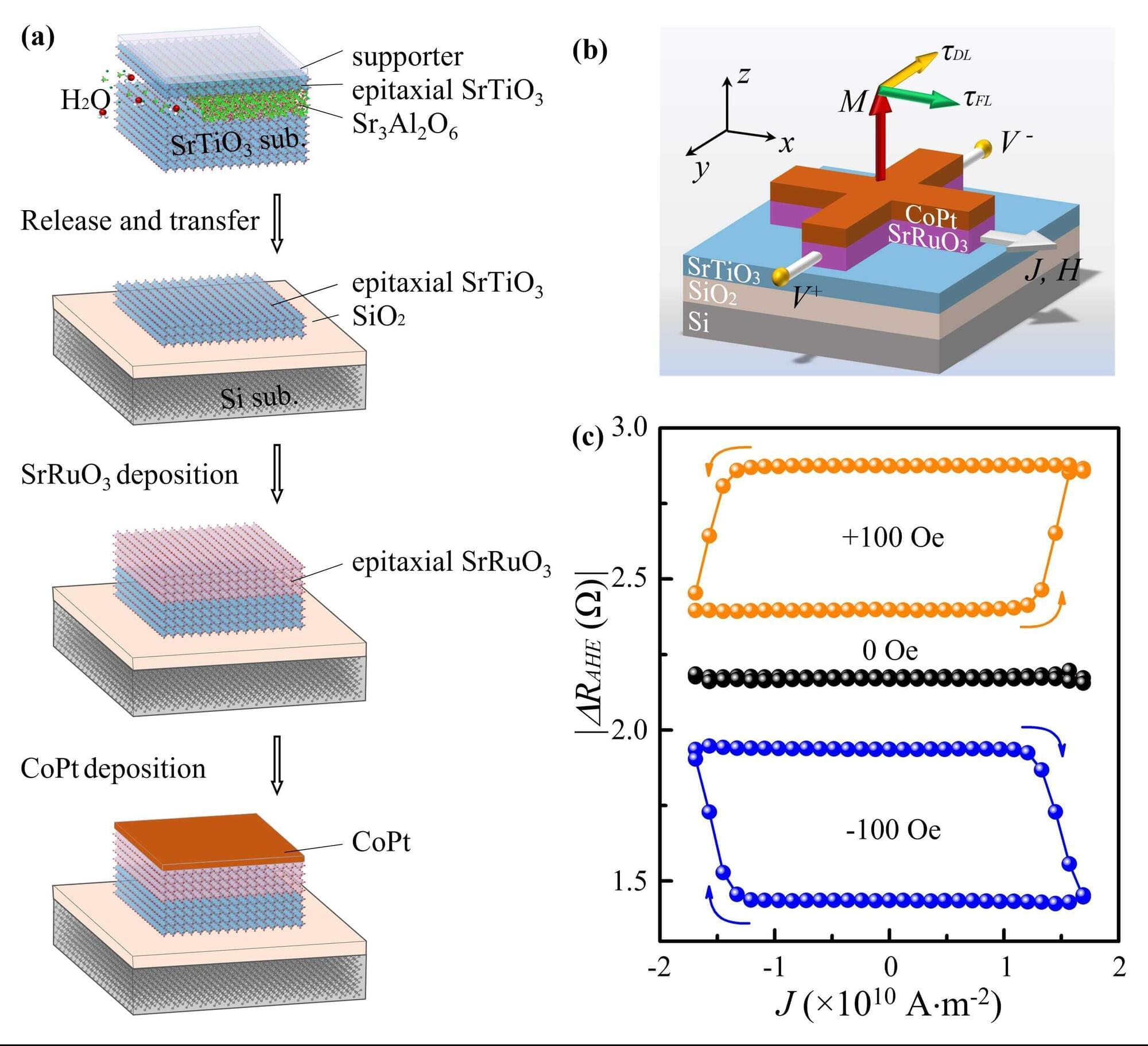
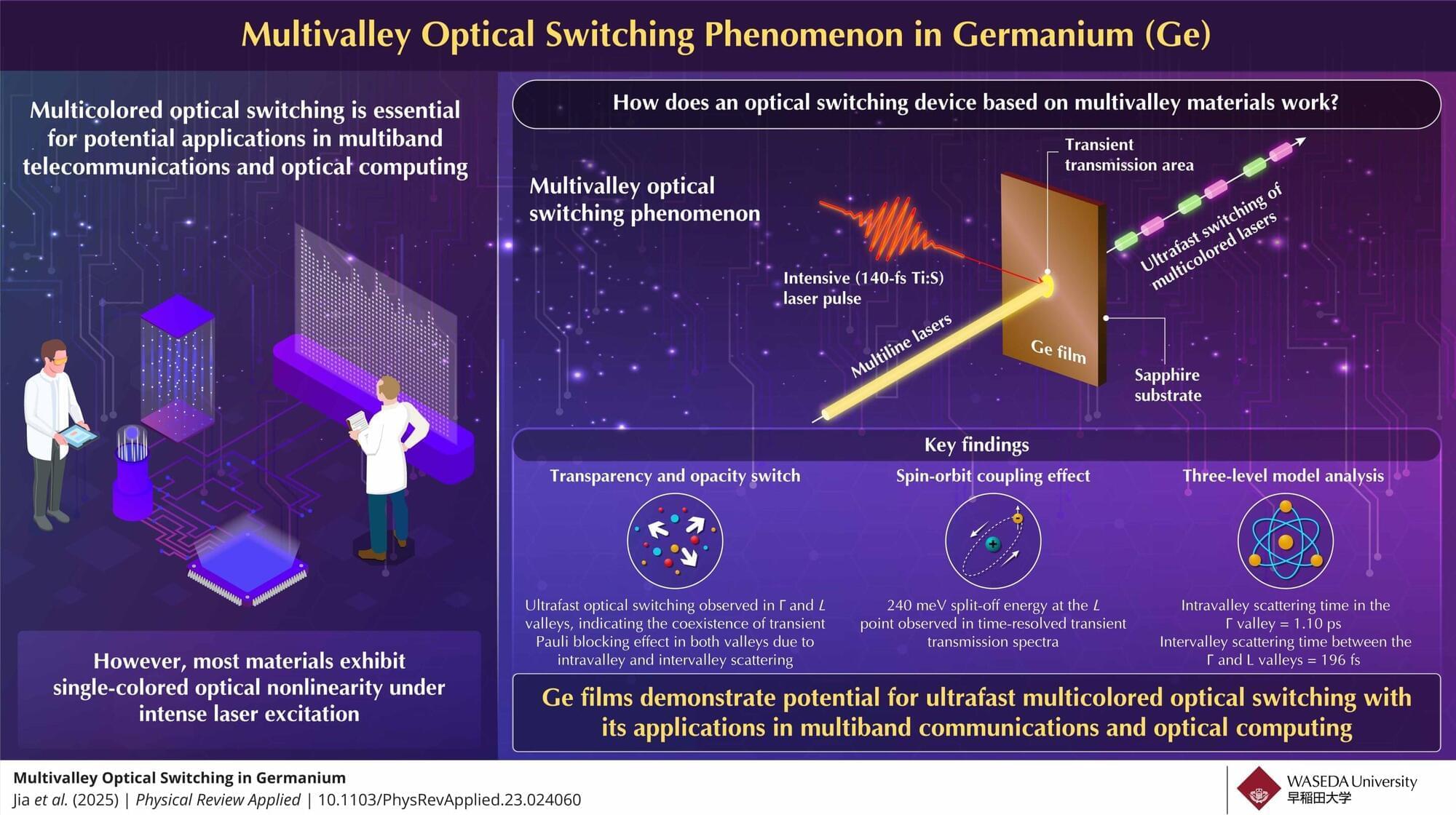
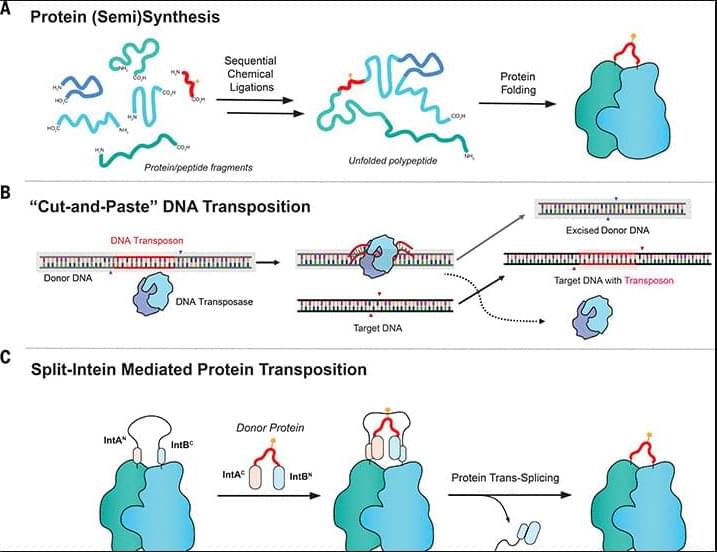
Controlling the uniformity in size and quantity of macroscopic three-dimensional (3D) DNA crystals is essential for their integration into complex systems and broader applications. However, achieving such control remains a major challenge in DNA nanotechnology. Here, we present a novel strategy for synthesizing monodisperse 3D DNA single crystals using microfluidic double-emulsion droplets as nanoliter-scale microreactors. These uniformly sized droplets can shrink and swell without leaking their inner contents, allowing the concentration of the DNA solution inside to be adjusted. The confined volume ensures that, once a crystal seed forms, it rapidly consumes the available DNA material, preventing the formation of additional crystals within the same droplet. This approach enables precise control over crystal growth, resulting in a yield of one DNA single crystal per droplet, with a success rate of up to 98.6% ± 0.9%. The resulting DNA crystals exhibit controlled sizes, ranging from 19.3 ± 0.9 μm to 56.8 ± 2.6 μm. Moreover, this method can be applied to the controlled growth of various types of DNA crystals. Our study provides a new pathway for DNA crystal self-assembly and microengineering.