As quantum advantage has been demonstrated on different quantum computing platforms using Gaussian boson sampling,1–3 quantum computing is moving to the next stage, namely demonstrating quantum advantage in solving practical problems. Two typical problems of this kind are computational-aided material design and drug discovery, in which quantum chemistry plays a critical role in answering questions such as ∼Which one is the best?∼. Many recent efforts have been devoted to the development of advanced quantum algorithms for solving quantum chemistry problems on noisy intermediate-scale quantum (NISQ) devices,2,4–14 while implementing these algorithms for complex problems is limited by available qubit counts, coherence time and gate fidelity. Specifically, without error correction, quantum simulations of quantum chemistry are viable only if low-depth quantum algorithms are implemented to suppress the total error rate. Recent advances in error mitigation techniques enable us to model many-electron problems with a dozen qubits and tens of circuit depths on NISQ devices,9 while such circuit sizes and depths are still a long way from practical applications.
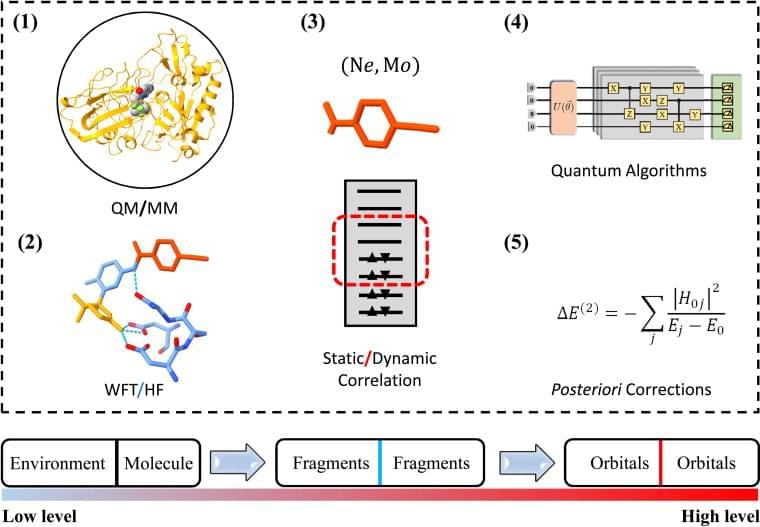
The difference between the available and actually required quantum resources in practical quantum simulations has renewed the interest in divide and conquer (DC) based methods.15–19 Realistic material and (bio)chemistry systems often involve complex environments, such as surfaces and interfaces. To model these systems, the Schrödinger equations are much too complicated to be solvable. It therefore becomes desirable that approximate practical methods of applying quantum mechanics be developed.20 One popular scheme is to divide the complex problem under consideration into as many parts as possible until these become simple enough for an adequate solution, namely the philosophy of DC.21 The DC method is particularly suitable for NISQ devices since the sub-problem for each part can in principle be solved with fewer computational resources.15–18,22–25 One successful application of DC is to estimate the ground-state potential energy surface of a ring containing 10 hydrogen atoms using the density matrix embedding theory (DMET) on a trapped-ion quantum computer, in which a 20-qubit problem is decomposed into ten 2-qubit problems.18
DC often treats all subsystems at the same computational level and estimates physical observables by summing up the corresponding quantities of subsystems, while in practical simulations of complex systems, the particle–particle interactions may exhibit completely different characteristics in and between subsystems. Long-range Coulomb interactions can be well approximated as quasiclassical electrostatic interactions since empirical methods, such as empirical force filed (EFF) approaches,26 are promising to describe these interactions. As the distance between particles decreases, the repulsive exchange interactions from electrons having the same spin become important so that quantum mean-field approaches, such as Hartree–Fock (HF), are necessary to characterize these electronic interactions.